Tam giác là loại hình học cơ bản và xuất hiện trong nhiều cấp bậc của chương trình học. Bên cạnh tính chất hay chu vi hình tam giác thì công thức tính diện tích các loại hình tam giác luôn được nhiều người quan tâm. Bài viết dưới đây sẽ cập nhật đầy đủ nhất về công thức tính diện tích tam giác. Mời các bạn cùng tham khảo!
Tìm hiểu về hình tam giác
Trước khi tìm hiểu về diện tích tam giác, bạn cần ghi nhớ những thông tin cơ bản cũng như tính chất của loại hình học này!
Hình tam giác là gì?
Hình tam giác là một đa giác có 3 cạnh và 3 đỉnh, đây là một loại hình học cơ bản trong toán học. Các cạnh của tam giác nối các đỉnh với nhau và các góc giữa các cạnh tạo thành các góc của tam giác.
Phân loại hình tam giác
Dựa vào các tính chất khác nhau mà tam giác được phân loại như sau:
Dựa vào số cạnh
- Tam giác cân: Có ít nhất hai cạnh bằng nhau.
- Tam giác đều: Có ba cạnh bằng nhau, ba góc bằng nhau và đều bằng 60 độ.
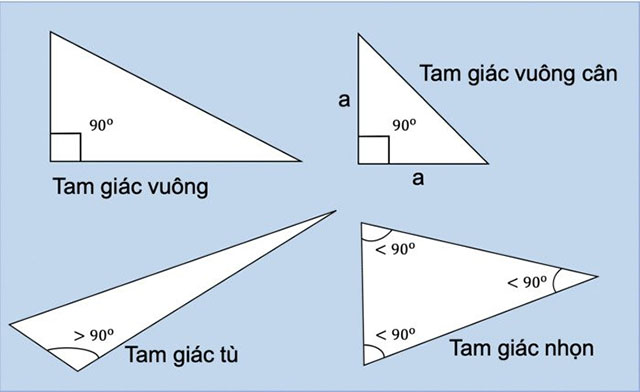
- Tam giác vuông: Có một góc vuông 90 độ.
Theo góc
- Tam giác tù: Có một góc tù (góc lớn hơn 90 độ)
- Tam giác nhọn: Có 3 góc nhọn và các góc đều nhỏ hơn 90 độ.
- Tam giác vuông: Có 1 góc vuông bằng 90 độ
Các loại hình tam giác
Theo độ dài các cạnh
- Tam giác đều: Có 3 cạnh bằng nhau
- Tam giác thường: Ba cạnh và ba góc không bằng nhau
Tính chất hình tam giác
- Tổng các góc: Tổng các góc trong một tam giác luôn bằng 180 độ.
- Góc ngoài tam giác: Mỗi góc ngoài của tam giác bằng tổng hai góc trong tam giác không chứa nó.
- Định lý Pythagoras: Trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.
- Đoạn phân giác của tam giác: Đoạn phân giác là đoạn thẳng từ một đỉnh của tam giác đến điểm trên cạnh đối diện, sao cho chia cạnh tam giác thành hai đoạn có tỉ số bằng tỉ số độ dài hai cạnh còn lại.
- Trung điểm trong tam giác: Ba đoạn thẳng nối các đỉnh của tam giác tới các điểm trung điểm của cạnh đối diện là ba đoạn thẳng có độ dài bằng nhau.
Tổng hợp công thức tính diện tích tam giác
Tùy theo từng loại tam giác mà cách tính diện tích sẽ khác nhau. Dưới đây là công thức chung của từng loại tam giác mà bạn có thể tham khảo!
Công thức tính diện tích tam giác thường
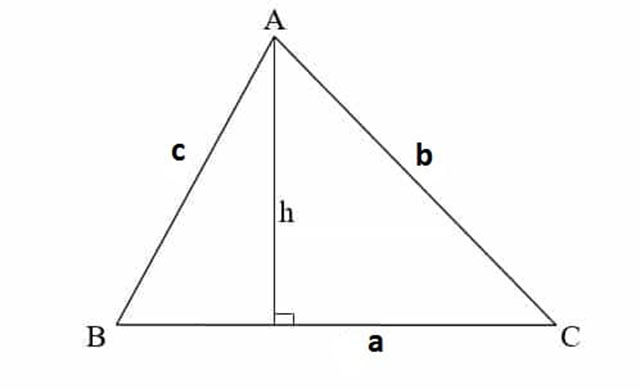
Tam giác thường
Diện tích tam giác thường được tính bằng cách lấy chiều cao của tam giác nhân với độ dài cạnh đáy sau đó chia hai. Cụ thể: S = (a x h)/2
Trong đó:
- h là chiều cao của tam giác
- a là cạnh đáy của tam giác.
Ví dụ: Cho tam giác ABC có chiều cao h là 8cm, độ dài cạnh đáy là 18cm. Bạn hãy tính diện tích hình tam giác ABC.
Áp dụng công thức ta có, diện tích tam giác ABC = (18 x 8) / 2 = 72cm2.
Công thức tính diện tích tam giác cân
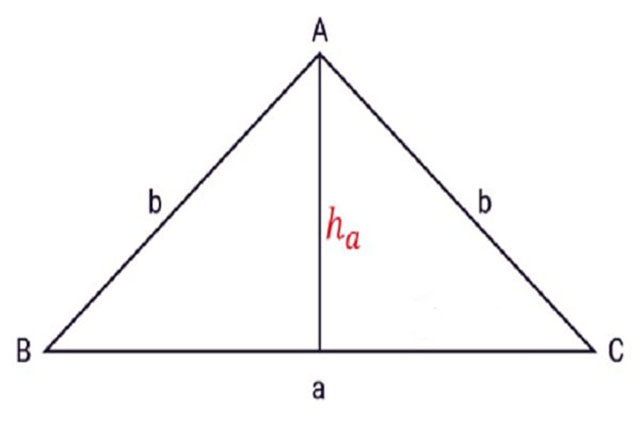
Hình tam giác cân
Diện tích tam giác cân được tính theo công thức một phần hai tích của chiều cao tam giác (đoạn thẳng nối từ đỉnh tam giác xuống cạnh đáy tam giác. Đoạn thẳng này phải hạ vuông góc với đáy tam giác).
Công thức như sau: S = (a x h) / 2
Trong đó:
- h: chiều cao tam giác
- a: chiều dài cạnh đáy của tam giác.
Ví dụ: Cho tam giác cân ABC như hình trên. Trong đó, các cạnh bên AB = AC = b = 6cm; cạnh đáy BC = a = 12cm và chiều cao hạ từ điểm A xuống cạnh đáy BC là h = 10cm. Bạn hãy tính diện tích hình tam giác ABC?
Giải: Theo đề bài đưa ra, diện tích tam giác cân ABC = (12 x 10) /2 = 60cm2
Công thức tính diện tích tam giác đều
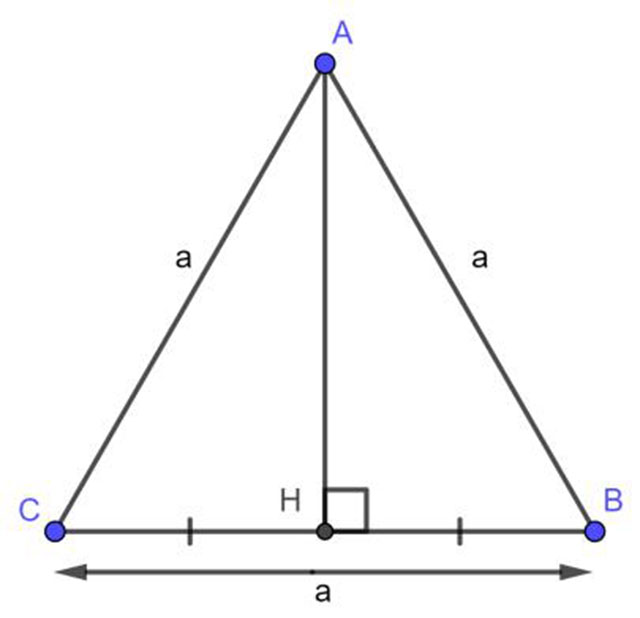
Hình tam giác đều
Tam giác đều là hình tam giác có ba cạnh bằng nhau, ba góc của tam giác có số đo bằng nhau và bằng 60 độ. Công thức tính diện tích tam giác đều được tính bằng tích chiều cao của tam giác nhân với chiều dài của cạnh đáy tam giác. Cụ thể:
S = (a x h) / 2. Trong đó:
- a: kích thước cạnh đáy của tam giác
- h: chiều cao của tam giác
ví dụ: Cho tam giác đều ABC như hình. Trong đó chiều dài cạnh đáy AB = BC = AC = 10cm, chiều cao AH = 6cm. Bạn hãy tính chiều cao của tam giác đều ABC.
Giải: Theo đề bài đưa ra diện tích của tam giác đều ABC = (10 x 6) / 2 = 30cm2.
Công thức tính diện tích tam giác vuông
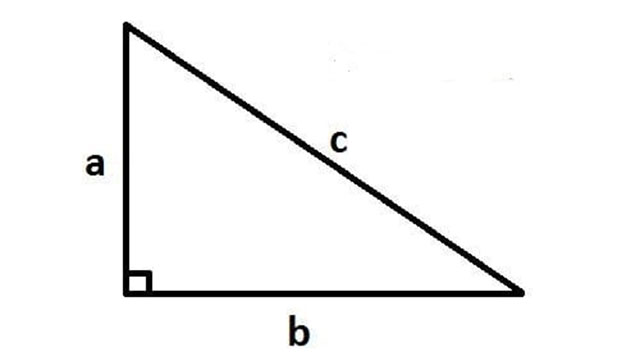
Hình tam giác vuông
Chiều cao của tam giác vuông sẽ trùng với một cạnh góc vuông trong tam giác, cạnh góc vuông còn lại là cạnh đáy. Công thức tính diện tích tam giác được xác định bằng một phần hai tích hai cạnh góc vuông.
Cụ thể: S = (a x b) /2
Trong đó:
- a là chiều cao tam giác vuông
- b là một cạnh của góc vuông
Ví dụ: Cho tam giác vuông như hình với chiều dài các cạnh góc vuông a = 5cm và b = 14cm. Bạn hãy xác định diện tích của tam giác vuông trên.
Giải: Theo đề bài đưa ra, diện tích của tam giác vuông = (4 x 14)/2 = 28cm2.
Công thức tính diện tích tam giác vuông cân
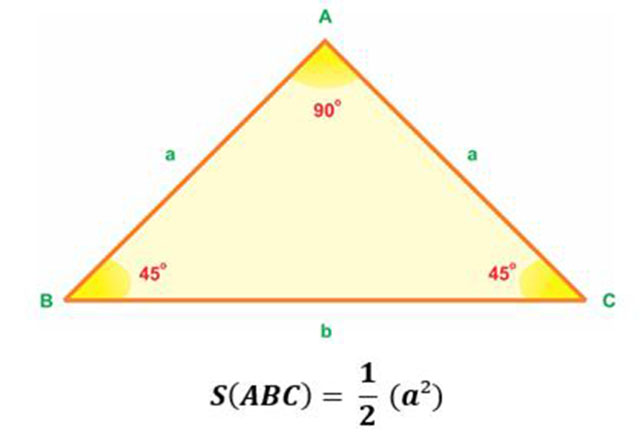
Công thức tính diện tích tam giác vuông cân
Diện tích của tam giác vuông cân được tính bằng độ dài một cạnh góc vuông bình phương sau đó chia hai. Cụ thể: S = ½ (a2)
Trong đó a được hiểu là độ dài hai cạnh góc vuông bằng nhau.
Ví dụ: Tam giác vuông cân ABC có độ dài hai cạnh góc vuông là 4cm. Tính diện tích tam giác vuông cân ABC.
Giải: Áp dụng công thức trên ta có diện tích của tam giác vuông cân ABC là 8cm2.
Công thức tính diện tích tam giác trong hệ tọa độ Oxyz
Trong hệ tọa độ Oxyz, tam giác là một đa giác ba cạnh nằm trong không gian ba chiều và được xác định bởi ba điểm không cùng một đường thẳng. Các điểm này được biểu diễn bằng các tọa độ (x, y, z). Trong đó x, y, z lần lượt là các số thực thể hiện vị trí của điểm trong không gian.
Công thức tính diện tích tam giác trong hệ trục tọa độ Oxyz được tính bằng nửa giá trị tuyệt đối của tích hạng ba của hai vectơ AB và AC.
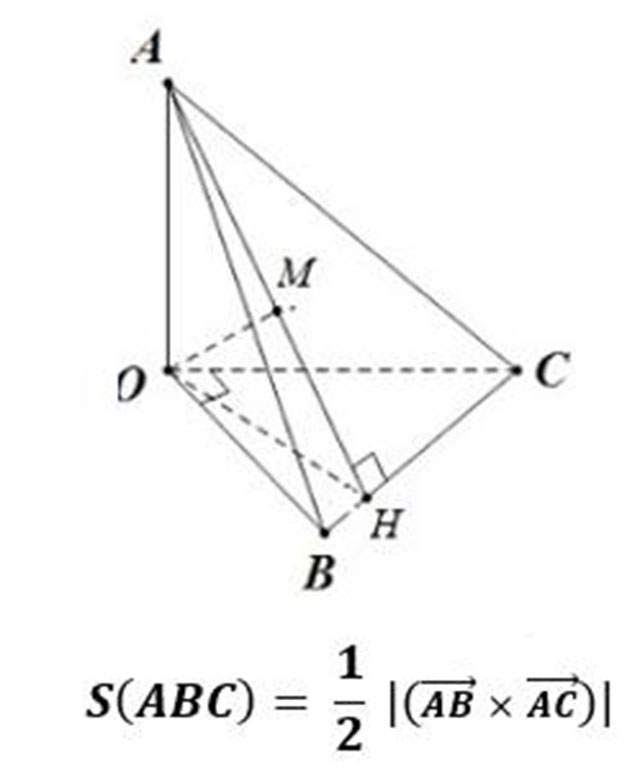
Công thức tính diện tích tam giác trong hệ tọa độ Oxyz
Trong đó: AB và AC là hai vectơ được biểu diễn trên trục Oxyz.
Ví dụ: Trên hệ trục tọa độ cho tam giác ABC có 3 điểm A(-1; 1; 2), B(1; 2; 3), C(3; – 2; 0). Diện tích tam giác ABC được tính như sau:
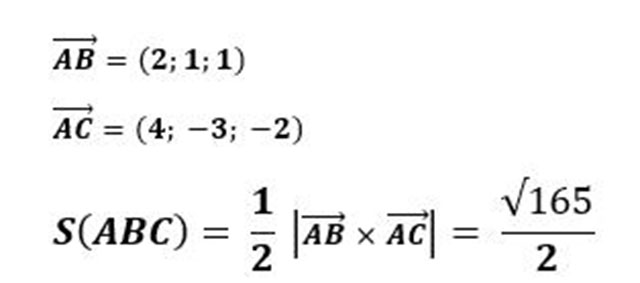
Diện tích tam giác trong hệ tọa độ Oxyz
Trên đây là tổng hợp diện tích tam giác cân, tam giác thường, tam giác vuông… đầy đủ nhất. Hy vọng với những thông tin trong bài viết sẽ giúp bạn dễ dàng hơn trong việc làm các bài tập liên quan đến hình tam giác.